
Para seleccionar una curva apropiada se comparó la curva representativa del proyecto analizado con varias curvas conocidas, pertenecientes a distintos sistemas eléctricos; una vez elegida la curva, se adoptó su ecuación. Se verificó lo razonable de la adopción cuando, al asignarle valores a los coeficientes de la ecuación, fueron satisfechos distintos puntos del esquema analizado (2). La ecuación representativa del Postulado del LMO corresponde a una curva exponencial asintótica (3, 4, 5, 6), cuya expresión es:
Donde M = valor de la mejora; L = valor del LMO; e = valor constante (2,718281828459...) (7), base de los logaritmos naturales; b = índice de concavidad; E = etapa analizada (en números enteros).
Como la curva representativa del proyecto analizado es una sucesión de segmentos, la ecuación no la satisface en todos sus puntos. Sin embargo, se cumple allí donde interesa (valores enteros sobre abscisas, representando a cada etapa).
Operando sobre la ecuación (a) se determina la ecuación para calcular el valor del LMO:

Se justifica la ecuación representativa del postulado analizando el estado estacionario y los teoremas de red (8) de un circuito serie Resistivo Inductivo (9).
Aplicando la ley de Kirchhoff de los voltages a un circuito Resistivo Inductivo (RL), se obtiene la ecuación diferencial:
 donde: L = inductancia; R = resistencia; E = fuerza electromotriz; i = corriente; t = tiempo. En cursos de Física se demuestra que si se aplica la fuerza E al circuito cuando t vale cero, la solución de la ecuación diferencial es:
donde: L = inductancia; R = resistencia; E = fuerza electromotriz; i = corriente; t = tiempo. En cursos de Física se demuestra que si se aplica la fuerza E al circuito cuando t vale cero, la solución de la ecuación diferencial es:
En el segundo miembro, el primer término representa el régimen permanente y el segundo término representa el régimen transitorio. Operando resulta:

- i(t) = M (mejoras).
- E/R = L (valor del LMO).
- R/L = b (índice de concavidad).
- t = E (etapa de valor unitario).
El factor exponencial hace que el régimen transitorio disminuya con el tiempo. Operando sobre el índice b se modifica la forma de la curva determinando mejores valores del LMO: esto demuestra lo dicho al tratar los Cambios Conceptuales y Trascendentes (CCT).
ÍNDICE DE CONCAVIDAD
La forma de la curva representativa del circuito eléctrico tomado como ejemplo es conocida y constante, ya que depende de los componentes físicos del circuito (Resistores, Inductores). Pero en el caso de la curva que representa a un proyecto no es así, pues al fijar las variables sobre los ejes coordenados se transfirieron las consecuencias de las Condiciones de Realización Existentes (CRE) a la curva.
La forma de la curva está representada por el Índice de Concavidad (índice b).
Cuando un Cambio Conceptual y Trascendente (CCT) modifica la pendiente y eleva la trayectoria de la curva, lo que se está realmente modificando es el valor del índice b.

Figura 1
Entonces, puede estimarse la tendencia del proyecto calculando los valores máximo, mínimo y promedio del Límite Máximo de Optimización, a partir de índices b adecuados. Los valores adoptados a continuación para igualar el denominador de la ecuación (b), fueron elegidos para posibilitar los cálculos.
Cuando el denominador de la ecuación (b) es lo más cercano posible a cero. Adoptando 0.1, resulta:
Operando, se calcula el índice b para L máximo: índice b = 0.1.
Este valor determina una curva de concavidad mínima: la mejora de la segunda etapa será empinada y rozará la prolongación de la primera etapa, pasando cerca de la semirrecta a.
Valor mínimo del LMO.
Cuando el denominador de la ecuación (b) es lo más cercano posible a uno. Adoptando 0.95, resulta:

Este valor determina una curva de concavidad máxima: la mejora de la segunda etapa será aplanada y pasará cerca de la semirrecta z.
Valor promedio del LMO.
Se considera un índice de concavidad intermedio: índice b = 1.5.
ANÁLISIS DE LAS MEJORAS DE LA PRIMERA ETAPA
También se indica en qué etapa (E) se alcanzaría el resultado deseado del 100% (el “0” significa que con ese porcentaje de mejora y ese índice b nunca se alcanzará el 100%). Algunos de los valores del LMO mostrados en la TABLA 1 superan el 100 %; se muestran como ejemplo de los cálculos y para destacar una particularidad que confirma la filosofía de los Cambios Conceptuales y Trascendentes: los valores más altos del LMO corresponden a curvas con pendientes elevadas (o sea, con índices b chicos).
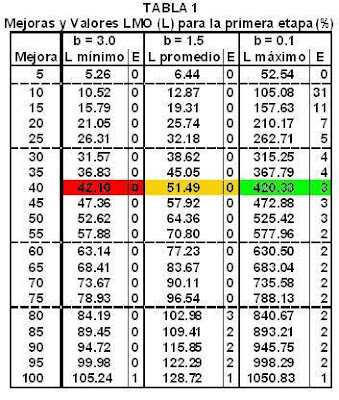 Para mejoras iniciales hasta el 25 %.
Para mejoras iniciales hasta el 25 %.De la TABLA 1 resulta:
- Si la mejora es menor del 10 %, en ningún caso se podrá alcanzar el resultado deseado (todo el proyecto debe replantearse).
- Si la mejora está entre el 10 % y el 25 %, solo bajo infrecuentes condiciones óptimas se podría alcanzar el 100 %, pero aún así se necesitarían demasiadas etapas (no hay coherencia entre condiciones óptimas y mejoras tan bajas, por lo que se debe revisar la implementación o replantear todo el proyecto).
Para mejoras iniciales superiores al 25 %.
Es necesario conocer el índice b de la curva representativa del proyecto (este valor podrá estimarse, ser copiado de proyectos anteriores similares, o calcularse al conocer la mejora de la segunda etapa):
- Si el índice b es elevado (b = 3), para tener valores del LMO cercanos al resultado deseado la mejora de la primera etapa debe ser del 80 % o mayor, y aún así se deben producir CCT (si la mejora no alcanza ese valor o si no se pueden producir los cambios necesarios, se deben cambiar las CRE y replantear todo el proyecto).
- Si el índice b es un valor promedio (b = 1.5) y la mejora está entre el 26 % y el 55 %, se deben producir CCT para obtener el resultado deseado (si los cambios no son suficientes se debe replantear el proyecto).
- Si el índice b es un valor promedio (b = 1.5) y la mejora está entre el 56 % y el 75 %, las CRE facilitan los CCT necesarios para alcanzar el resultado deseado (si el evaluador estima que no es así, deberá replantear el proyecto).
- Si el índice b es un valor promedio (b = 1.5) y la mejora es mayor del 75 %, el resultado deseado se alcanzará naturalmente en 1, 2 o 3 etapas, dependiendo del valor de la mejora.
VALORES DEL ÍNDICE DE CONCAVIDAD (b)
La TABLA 1 presenta valores del LMO para tres índices b diferentes, pero en la realidad la forma de la curva representativa de un proyecto puede tomar cualquier valor entre los valores mínimo y máximo planteados.
No olvidar que cuando se igualó el denominador de la ecuación (b) a un valor cercano a cero se adoptó 0.1 y que al igualar ese denominador a un valor cercano a uno se adoptó 0.95. Para los casos comunes los valores adoptados son suficientes, pero podrían necesitarse mayores precisiones al analizar temas científicos (adoptar valores cercanos a cero y menores de 0.1 o valores cercanos a uno y mayores de 0.95).
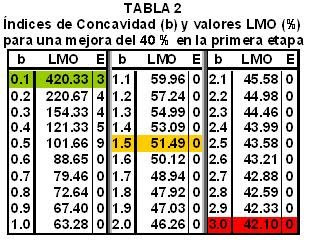
En la TABLA 2, generada por un programa de computación, para una mejora de la primera etapa del 40 % se muestran los índices b en intervalos de 0.1, los valores del LMO obtenidos según cada índice b y la etapa (E) en que se alcanzará el resultado deseado del 100 %.
Los datos de la TABLA 2 son importantes para el evaluador: le permiten pronosticar la forma de la curva y conocer la intensidad que deberán tener los CCT para modificar la tendencia y alcanzar el resultado deseado. Sabiendo si estos cambios son posibles podrá aceptar su realización o decidirá replantear todo el proyecto.
LMO A PARTIR DE LA SEGUNDA ETAPA
Todas las etapas, excepto la primera, conocen la historia de la curva por sus etapas anteriores. En cada etapa, al combinar datos anteriores y datos actuales se calcula un índice b ajustado a la realidad de esa etapa. Con los índices calculados en las sucesivas etapas se van determinando valores del LMO cada vez más probables. Esta metodología permite controlar en forma permanente la evolución de un proyecto pues actualiza en cada etapa el pronóstico sobre su resultado final, advirtiendo sobre las mejoras o deterioros producidos.
En cada etapa (n), los únicos datos que se tienen son:
- Mejora total alcanzada en la etapa anterior: Mn-1
- Mejora total alcanzada en la etapa actual: Mn
- Mejora aportada por la etapa actual. Se reducen los errores de estimación calculando este valor por diferencia entre las mejoras totales alcanzadas actual y anterior: Mn - Mn-1
FACTOR DE FORMA (f)
Para relacionar los datos existentes con la ecuación (a) conocida y determinar el índice b se calcula un dato intermedio, el Factor de Forma, definido como la mejora aportada por la etapa actual sobre la mejora total alcanzada en la etapa actual:

Determinación del índice de concavidad b de cada etapa
El Factor de Forma relaciona la pendiente de la etapa actual con la pendiente resultante de todas las etapas anteriores, y se asocia al régimen transitorio. El término exponencial de la ecuación (a) también se asocia al régimen transitorio. Igualando y operando:
REFERENCIAS
- B C Kuo, Automatic Control Systems (Cía. Editorial Continental S.A., México DF), 1965, Edición autorizada por Prentice Hall, Inc, Englewood Cliffs, N.J.), (2.1).
- P F Smith and A Sullivan Gale, Elements of Analytic Geometry (Librería-Edit. Nigar, Buenos Aires, 1955, Edición autorizada por Ginn & Co, Boston, USA), Capítulo III, Sección 32.
- F. Cernuschi y F. I. Greco, Teoría de Errores de Mediciones (Editorial Universitaria de Buenos Aires, Argentina, 1974), Capítulo V-6 (Ajuste de curvas).
- Staff Members of the Massachusetts Institute of Technology, Electric Circuits. Cía. Ed. Continental SA, México DF, 1963, autorizado por John Wiley & Sons, Inc, NY,3-6.
- F W Sears, Electricity and Magnetism (Ed. Aguilar, Madrid, 1959, autorizada por Addison-Wesley Publishing Co, Inc, Reading, Massachusetts), Capítulos 8-5 y 13-3.
- W. L. Everitt and G. E. Anner, Communication Engineering (Editorial Arbó S.A.C.I., Buenos Aires, 1961, Edición autorizada por McGraw-Hill Book Co, Inc), Cap. II-14.
- Tablas Científicas, Ciba-Geigy S.A., Basilea, Suiza, 6° Edición, 1973, (I).
- ibid 6., Capítulo III.
- ibid 4., Capítulo III-4.
Contacto: CienciaAplicada.jgs@gmail.com


